「ポケモンを確実に見つける方法」をExcelで数学してみた

最終更新日：2016-11-04

「ポケモンを確実に見つける方法」をExcelで数学してみた

ポケモンGO関連の記事をみていたら、

【ポケモンGO】かくれているポケモンを確実に見つける方法、という記事を読んだ。

普通にそうだなという感想なのですが、

もっとまじめに数学したら、もっと良い方法があるのではないかと。

元記事はあちこちで見た気がするが、多分これでしょ
「【ポケモンGO】かくれているポケモンを確実に見つける方法」
で探せば、直ぐに見つかります。

そこでの方法としては
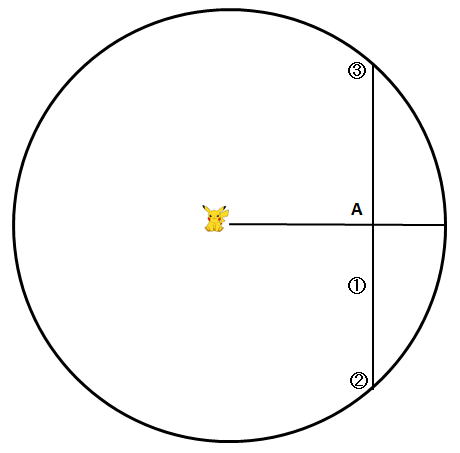
Excel ポケモンGO

近くにいるポケモンに表示された地点を①
そこから、どっちの方向でも良いので真っ直ぐに進みポケモンが消える地点を②
今度は真逆に歩いて、ポケモンが表示されて、そして消える地点を③
※②から③までの距離を歩数等で測っておく
②と③の中間点Aを、直角に左右のどちらかに進めばポケモンがいる。

確かに、この考え方なら小学生でもわかる理屈です。
しかし、最後が2択になってしまい、反対に歩き出してしまうとかなり距離をロスしますね。
原因は、一直線に歩くからなのですか、
ちゃんと数学すれば、もっと確実にポケモンにたどり着けるのではないかという事で考えてみました。

高校生くらいになれば、もっとちゃんと数学できるでしょ、ということで、
もっと高度に、最短距離でポケモンにたどり着く方法を数学してみました。

まずは、

歩き方

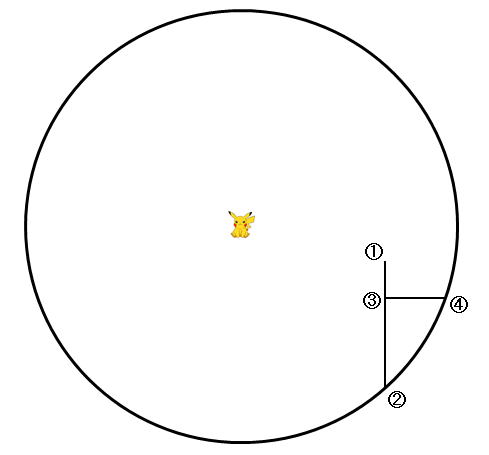
近くにいるポケモンに表示された地点を①
そこから、どっちの方向でも良いので真っ直ぐに進みポケモンが消える地点を②
今度は真逆に歩いて、ポケモンが表示されてから、もう少し進んだ地点を③
※ここが重要、①まで戻る必要はない、ポケモンが確実に表示された地点で良い。
※②から③までの距離を歩数等で測っておく
③の地点を、直角に左右のどちらか（上図では右）に進んで、ポケモンが消える地点を④
※③から④までの距離を歩数等で測っておく
ここです、この時点（②と④の地点を特定した時点）で、ポケモンの場所は特定されています。

ポケモンの場所を特定できる理由

二点を通る円で半径R（200m）の円は2つだけ。
この場合は、①③を内に含まなければならないので円は一つだけ。
つまり、円が特定されるので、中心点も特定できるという事です。
念の為書いておくと、
②と④を中心に、半径R（200m）の円を書いた交点が、二点を通る円の中心になります。
小学校で、コンパス使って良くやったやつですね。

さて、ここからがちょっと難しくなります。
④の地点から、ポケモンの場所へ進むには、どうすれば良いか。
距離は半径R（200m）で間違いない。
後は、方角だけです。
④の地点から、②の地点を向いて、何度の角度で歩き出せば良いかを計算します。
つまり、②と④と円の中心（ポケモンの場所）の角度が分かれば良いのです。

数学の始まり

ここからが数学になります。
ここが重要です。
補助線を引いてみましょう。

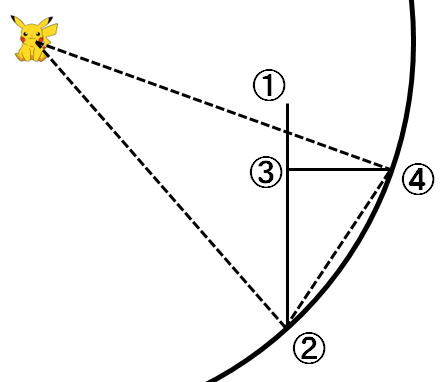
Excel ポケモンGO

円の中心から②④へ補助線を引いて、②と④の間にも引いてみます。
これで二等辺三角形の出来上がりです。

三角形だけを見てみると、

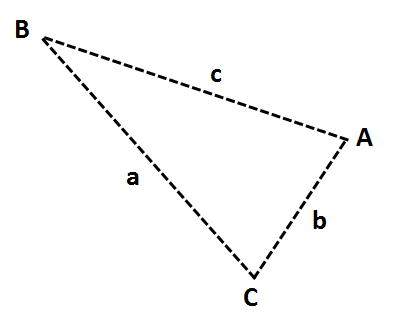
Excel ポケモンGO

辺AB(b)の長さは、半径(200m)です。
辺BC(a)の長さは、半径(200m)です。

辺AC(b)の長さは、②④の距離になるので、

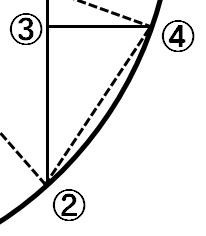
Excel ポケモンGO

超有名な定理、ピタゴラスの定理（三平方の定理）を使って、
②④二乗 = ②③二乗 + ③④二乗
これで求まります。

三角形の3辺の長さが求まれば、
余弦定理
これで計算できます。

すみません、
余弦定理の理屈までは、ちょっと説明できません。
私は現役退いて長いので、さすがに余弦定理までは・・・
多分、高1か高2くらいの数学だったはず。

Excelで計算してみた

bの計算式は、
=SQRT(B4^2+B5^2)
(②③二乗 + ③④二乗)の平方根

角Aの計算式は、
=DEGREES(ACOS((B3^2+B4^2-B2^2)/(2*B3*B4)))

ACOS関数

アークコサイン
ACOS(数値)
そのコサインが数値であるような角度をラジアンで返します。

DEGREES関数

ディグリーズ
DEGREES(角度)
ラジアンを度に変換します。

余弦定理を使った数式については、
ググって、あちこち見て回った計算式を、Excelの関数で作成しました。
多分あっているとは思うのですが、胸を張って言える程の自身は無いです。

上記では、
②③を80m
③④を70m
としたときの結果です。

つまり、

④の地点から、②の地点を向いて、
74.6度の方向に200m行った地点にポケモンがいるという事になります。

以上が、ポケモンの場所を特定する最短の歩き方と、ポケモンの位置を特定する方法です。
では、
このExcelを持って、スマホとともにポケモン探しへGO!
なんてことをしちゃダメですよ、絶対にダメね。

私は、これを書いている時点では、ポケモンGOは、もうちょっとで20レベルといったところなので、
ポケモンGO自体は、そんなに詳しくありませんので、あくまで机上での計算という事です。
ポケモンGOのGPSって、そんなに精度は良くないですしね。

そもそも、
200mも直進出来る場所が、この狭い日本にどれだけあるのか・・・
という基本的な疑問が大いにあります。
といいますか、
大抵は建物等に邪魔されて、目的地に着いた頃にはポケモンはいずこ・・・
ということで、あくまで机上のお遊びです。

高校生諸君、「数学なんて将来何の役に立つんだ」と思う事もあるでしょう。
その答えは、
こういう時に役に立ったり、立たなかったり
とにかく一生懸命勉強しましょう。